The Location Management of a mobile network is a major problem nowadays. One of the most popular strategies used to solve this problem is the Reporting Cells. To configure a mobile network is necessary to indicate what cells of the network are going to operate as Reporting Cells (RC). The choice of these cells is not trivial because they affect directly to the cost of the mobile network. We have to solve the Location Management, placing optimally the RC in a mobile network, minimizing its cost.

    The Reporting Cells planning was proposed by Bar-Noy and Kessler with the objective of minimizing the cost of tracking mobile users.

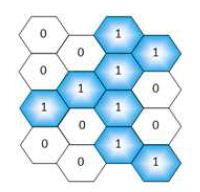
Fig. 1. RC (1) and nRC (0)

    According to the Reporting Cells scheme, there are two types of cells: reporting cells (RC) and non-reporting cells (nRC), as shown in Fig. 1. For all cells, RC and nRC, the vicinity factor is related by computing the maximum number of neighbour cells that must be paged if an incoming call occurs. Concretely, the vicinity factor of a single RC is given by the number of nRC accessible from this RC, without crossing any other RC and taking into account itself. On the other hand, the vicinity factor of a nRC is given by the maximum value of the vicinity factors of the RC’s accessible from this nRC. This means, if a nRC has more than one neighbouring RC, it must perform this process for each of them, using the highest value of vicinity factor.

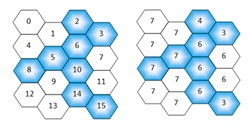
Fig. 2. Reporting Cells Planning

    As an example, in Fig. 2, the neighbouring cells of the cell 10 are the cells 7, 9, 11, 12, 13 and the own cell 10. Then, the value of the vicinity factor is 6, as it has six neighbouring cells (counting itself). On the other hand, if we see the cell 4, we have the cells 2, 5, 6 and 8 as neighbouring reporting cells, with vicinity factors 4, 7, 6, and 7, respectively. To calculate the Location Management cost we must select the highest value among them. In this case, the vicinity factor of the cell 4 is 7.   

    Location Management includes two elementary operations when calculating the total cost: location updates (LU) and location inquiries/paging (P), causing updating and paging costs respectively. The updating cost is caused by the sum of the costs of updating the terminals location in the network when they change their location and must register another one. The paging cost is caused by the network during a location inquiry when the network tries to locate a user and, normally, the number of paging transactions is directly related to the number of incoming calls.  

  The cost of the location updates is given by NLU, the cost of the location paging is given by NP, and finally, β is a constant that denotes the cost ratio of location update to a paging transaction in the network. It is proved that the updating cost is usually much higher than paging cost. For this, the updating cost is usually considered about 10 times greater than the paging cost, therefore β=10.
    We get the following formula to calculate the location management cost of a particular reporting cells configuration:

    Where NLU (i) is the number of location updates for Reporting Cell number i, S is the set of cells defined as reporting cells, the number of arrived calls for cell i is NP (i), N is the total number of cells in the network, V (i) is the vicinity factor for cell i and, finally, β is a constant representing the cost ratio of a location update to a paging transaction in the network, as described earlier. In conclusion, given a mobile network, the goal is to select which of their cells must act as RC to obtain the lowest possible cost.